ทำไมต้องทำ Ppk (Process Performance Index)

เราลองมาทำความรู้จักกับ Core tool ชนิดหนึ่งที่มีชื่อว่า Ppk

Ppk (Process Performance Index) ,(k : Katayori การเปลี่ยนหรือการเลื่อน) คือ การประเมินความสามารถของกระบวนการ ระหว่าง ชิ้นงานจริงที่เราผลิตได้กับ สเปกที่ลูกค้ากำหนดใน Drawing (USL,LSL) ในช่วงทดลองผลิต (Trial Run) ซึ่งอาจทำให้กระบวนการยังไม่เสถียร (Not-Stable) ซึ่งจะมีความแตกต่างจาก Cpk เนื่องจาก Cpk นั้นจะเป็นการประเมินความสามารถของกระบวนการ ในช่วง Mass Production
คำนิยามระหว่าง Cpk และ Ppk

1. ค่า Cpk และ Ppk เป็นการนำค่าเฉลี่ยของ กระบวนการ ค่าความผันแปรของกระบวนการและข้อ กำหนดของลูกค้ามาคำนวณร่วมกัน ดัชนีชี้วัดดังกล่าว สะท้อนว่ากระบวนการมีขีดความสามารถแค่ไหนเมื่อเทียบ กับข้อกำหนดของลูกค้า
2. Cpk เป็นค่าที่บอกถึงขีดความสามารถของ กระบวนการในระยะสั้น คือ ที่เวลาใดเวลาหนึ่งกระบวนการ มีขีดความสามารถเป็นอย่างไร
3. Ppk เป็นค่าที่บอกถึงขีดความสามารถของ กระบวนการในระยะยาวซึ่งจะรวมเอาความผันแปรที่เกิด จากความไม่มีเสถียรภาพของกระบวนการเข้ามาด้วย กล่าวคือ มีความ ผันแปรระยะสั้นรวมกับความผันแปรอื่นที่เข้ามากระทบกระบวนการ
4. ค่า Ppk จะน้อยกว่าหรือเท่ากับ Cpk เสมอ
5. ถ้า Cpk และ Ppk มีค่าใกล้กัน แสดงว่ากระบวนการไม่สูญเสีย เสถียรภาพเนื่องจากการขยับตัวของค่าเฉลี่ยหรืออาจกล่าวได้ว่ากระบวนการ ถูกควบคุมได้อย่างมีเสถียรภาพในระยะยาว ซึ่งกรณีตรงกันข้าม ถ้าค่า Ppk น้อยกว่า Cpk มาก แสดงว่ากระบวนการสูญเสีย เสถียรภาพ

อย่างที่อุตสาหกรรมวงการต่างๆทราบกันดีว่า การประเมินความสามารถของกระบวนการ (Cpk,Ppk) นั้นมีความสำคัญกับผลิตภัณฑ์ที่ออกมา และเพื่อให้ได้ข้อมูลที่สามารถยอมรับได้ทั้งลูกค้า และผู้ผลิต แต่ก่อนจะมีการประเมินความสามารถของกระบวนการ ต้องรู้จักการทำ Control Chart ด้วย

Control Chart คือแผนภูมิที่ แสดงคุณลักษณะของกระบวนการจากข้อมูลที่บันทึกลงไป เพื่อประเมิณว่ากระบวนการดังกล่าวอยู่ภายใต้สภาวะควบคุมทางสถิติ หรือไม่ และช่วยในการรักษาสภาวะที่ควบคุมได้ทางสถิติ โดยมักจะมีการตรวจวัดจุด SC (Special Characteristics)  หรืออาจเป็นจุดที่พบปัญหาด้านคุณภาพบ่อย

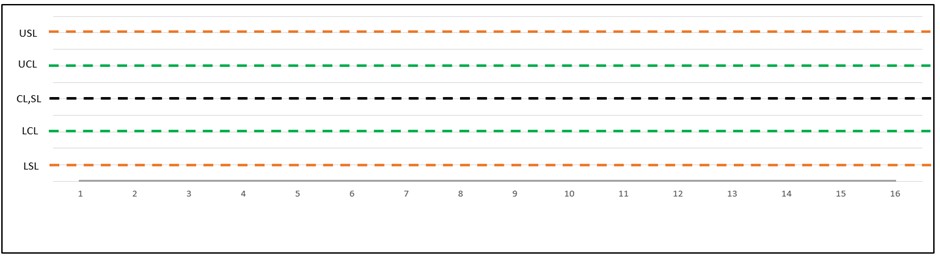
ซึ่งแผนภูมิของ Control Chart จะประกอบไปด้วย

1. Upper Control limit : UCL (ค่าสูงสุดที่ยอมรับได้)
2. Center line : CL (ค่าที่วัดได้,ค่าเฉลี่ย หรือ ค่ากลาง)
3. Lower Control limit : LCL (ค่าต่ำสุดที่ยอมรับได้)
4. Upper Specification limit : USL (ค่าสูงสุดที่ลูกค้ากำหนด)
5. Specification limit : SL (ค่าที่วัดได้,ค่าเฉลี่ย หรือค่ากลางที่ลูกค้ากำหนด)
6. Lower Specification limit : LSL (ค่าต่ำสุดที่ลูกค้ากำหนด)

หน้าที่ของ Control Chart คือ การแยกความผันแปรที่เกิดขึ้นโดยผิดธรรมชาติ และ เกิดขึ้นโดยธรรมชาติ ซึ่งความผันแปรดังกล่าวสามารถเกิดได้ทั่วไป ถึงแม้เครื่องมือหรือชิ้นงานจะเหมือนกัน ซึ่งความผันแปรทั้ง 2 แบบมีความแตกต่างกันอย่างไรและปัจจัยที่ทำให้เกิดมีอะไรบ้าง

1. ความผันแปรที่เกิดขึ้นโดยธรรมชาติ (Common Cause) จะเกิดขึ้นอยู่ตลอดเวลา สามารถคาดการณืได้ ไม่สามารถแก้ไขได้ แต่สามารถควบคุมให้อยู่ในเกณฑ์ยอมรับได้ ยกตัวอย่างเช่น

1.1. ความเมื่อยล้าของพนักงาน

1.2. แรงเสียดทานภายในเครื่องจักร

1.3. ความแตกต่างของวัตถุดิบ

2. ความแปรที่เกิดขึ้นโดยผิดธรรมชาติ (Special Cause) ไม่สามารถคาดการณ์ได้ แต่สามารถแก้ไขหรือกำจัดได้ ยกตัวอย่างเช่น

2.1 ปรับตั้งเครื่องจักรผิด

2.2 พนักงานไม่ทำตามมาตรฐานที่กำหนด

2.3 วัสดุที่ใช้ในการผลิต ผิดมาตรฐาน

2.4 เครื่องจักรทำงานผิดปกติ หรือชำรุด

เพราะฉะนั้น Control Chart จะแสดงให้เห็นว่าความสามารถของกระบวนการของเรามีข้อบกพร่องในส่วนไหนบ้าง และข้อบกพร่องที่เกิดขึ้นเกิดจากสาเหตุอะไรและสามารถควบคุมได้หรือไม่ ในกรณีที่เกิดความผันแปรที่ผิดธรรมชาติ (Special Cause) เป็นไปได้ว่า 4M ภายในองค์กรณ์ต้องมีความผิดปกติเกิดขึ้น

ตัวอย่างกราฟ Control Chart

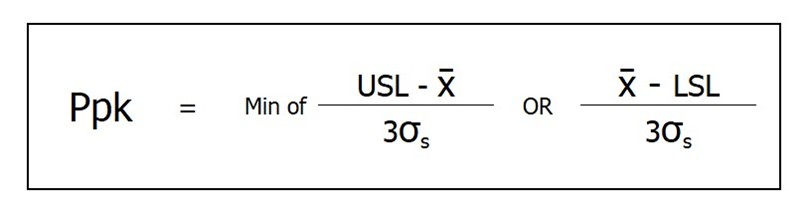
สูตรการคำนวณค่า Ppk

σ_s คือ S หรือ SD (Standard Deviation) ค่าส่วนเบี่ยงเบนมาตรฐานค่าที่ใช้แสดงความแม่นยาของการวัดซ้ำหลายๆครั้งหรือหลายตัวอย่าง

ยกตัวอย่างการคำนวณหาค่า σ_s หรือ S หรือ SD (Standard Deviation)

โดยความหมายของสูตรมีดังนี้

ชิ้นงาน มีขนาดความยาว 20 และ Toralance ± 2.0 ค่าที่วัดได้เท่ากับ 16,15,20,26 และ 17 จากสูตรด้านบนคำนวนได้ดังนี้

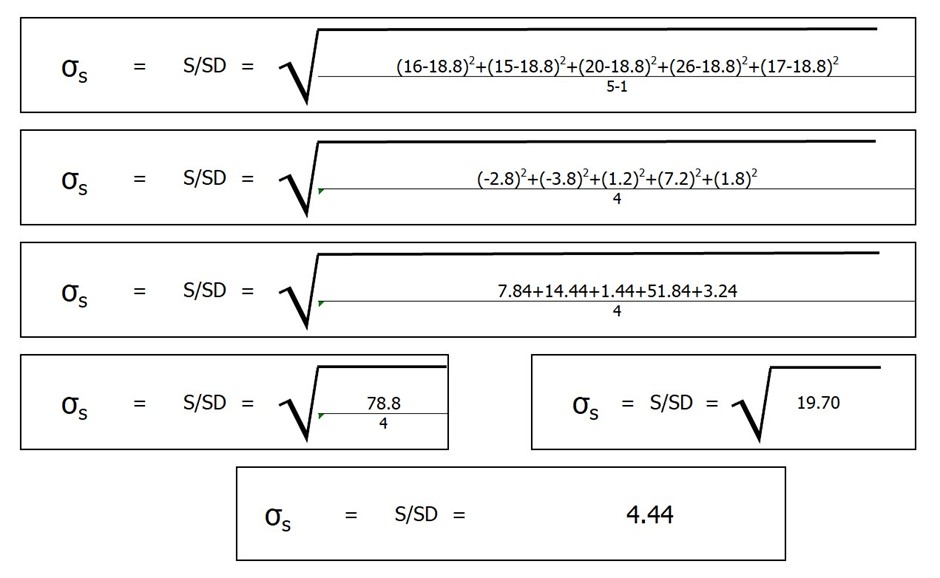
เพราะฉะนั้นจากตัวอย่าง ค่า σ_s จะมีค่าเท่ากับ 4.44

ยกตัวอย่างการคำนวณหาค่า Ppk

บริษัท M และ บริษัท C ได้รับชิ้นงานสเปคเดียวกันมาผลิตและได้มีการเก็บตัวอย่างบันทึกผลครั้งละ 5 ชิ้นจำนวน 10 ชุดตัวอย่าง เพื่อบันทึกผล ซึ่งชิ้นงานมีค่า Diameter 35.0 และ Toralance ± 2.0

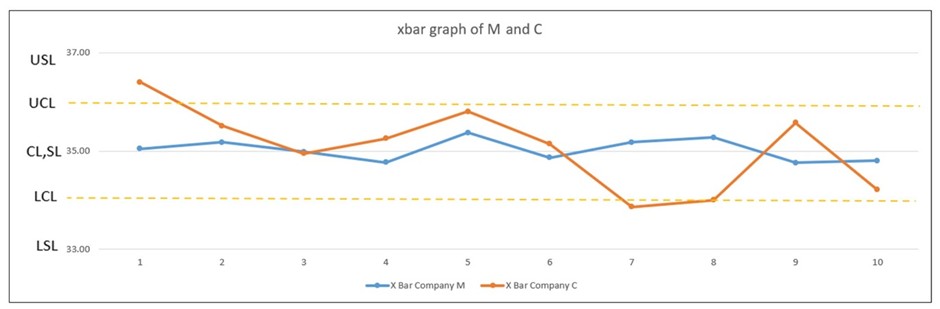
ค่า X bar ของทั้งสองบริษัทที่วัดได้

ค่า R Chart ของทั้งสองบริษัทที่วัดได้

และส่วนเบี่ยงเบนมาตรฐานของทั้ง 2 บริษัทที่ได้ มีค่าเท่ากับ 0.22 และ 0.83

หลังจากนั้นให้นำตัวเลขที่ได้จากการวัดและคำนวนมาใส่ลงในตัวแปรของแต่ละค่าดังนี้

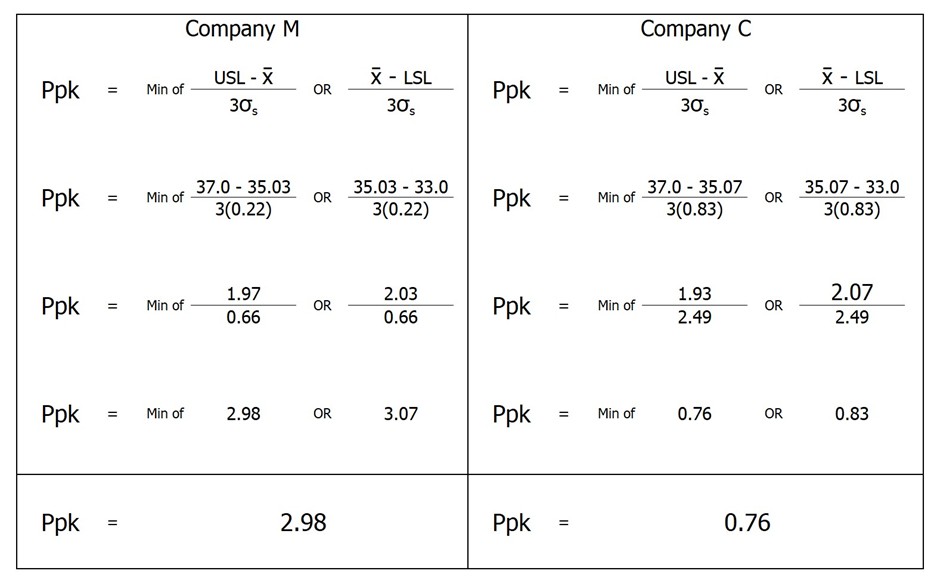
หลังจากนำมาคำนวณตามสูตร

เกณฑ์การประเมิณค่า Ppk

• Ppk < 1 กระบวนการมีขีดความสามารถที่ไม่ดี ควรได้รับ การปรับปรุง
• 1 < Ppk < 1.33 Gray Zone อาจพอรับได้ถ้ากระบวนการ นั้นควบคุมได้ยากหรือมีความจำกัดด้านเทคโนโลยี อย่างไรก็ตามถ้าเป็น ไปได้ควรปรับปรุงกระบวนการ
• Ppk > 1.33 กระบวนการมีขีดความสามารถอยู่ในเกณฑ์ ที่ดี
• Ppk > 2 คุณภาพระดับ World Class Quality หรือ Six Sigma Quality

จากค่า Ppk ที่ได้นั้นจะเห็นว่าชิ้นงานที่มีโอกาสจะได้รับการยอมรับจากลูกค้ามากที่สุดคือชิ้นงานจากบริษัท M ทั้งนี้จากตารางคำนวณจะเห็นได้ว่าค่า Xbar ไม่สามารถสรุปได้ว่าชิ้นงานที่สุ่มตรวจนั้นมีผลที่น่าพึงพอใจหรือไม่ จึงทำให้มีการนำ Ppk เข้ามามีส่วนเกี่ยวข้องในการประเมินความสามารถของการผลิตชิ้นงานนั้นๆ